Solve ABSOLUTE VALUE equations
When solving an absolute value inequality, replace
the | STUFF | with ± ( STUFF ),THUS , we split the inequality into two statements,
and solve them as an or or and statement.
Graph the and statements as an overlapping region,
and the or statements as two pieces going in opposite directions.
Example 1: Solve |3x-1| < 2. ----- THIS WILL BE AN AND TYPE
Replacing the | 3x-1 | symbols with ± ( 3x-1 ), we see
± ( 3x-1 ) < 2 This splits into 3x-1 < 2 AND - (3x-1) < 2
For the statement on the right, divide by -1 and reverse the < symbol.
3x-1 < 2 and 3x-1 > -2 NOW SOLVE EACH
x < 1 and x > -1/3 graph the INTERSECTION (OVERLAPPING
Example 2 Solve | 5x - 2| > 17
Replacing the | 5x-2 | symbols with ± ( 5x-2 ), we see
± ( 5x-2 ) > 17 This splits into 5x-2 > 17 OR - (5x-2) > 17
For the statement on the right, divide by -1 and reverse the < symbol.
5x-2 > 17 OR 5x-2 < -17 NOW SOLVE EACH
x > 3.8 OR x < -3
graph the









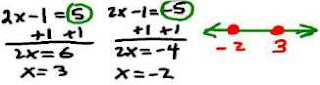






Comments
Post a Comment